細胞計數杯的結構形態、使用原理與應用前景
細胞計數杯是針對傳統細胞計數方法存在的問題設計的。細胞計數的正確含義是檢測細胞樣本的細胞密度,即單位體內的細胞數,不是單純計量細胞數。細胞密度由檢測樣本中細胞數和樣本體積兩個因素構成,兩者都準確細胞密度才準確。目前有代表性的三類細胞計數儀都沒有解決好細胞密度的問題。1.傳統細胞計數板的問題是計數的細胞樣本體積不準確。細胞計數板的計數池體積標定為1.0mm×1.0mm×0.1mm=0.1微升,深度不包括計數池與蓋玻片之間的空隙,空隙大小不確定。實際計數樣本是充滿計數池與蓋玻片之間的空間,所以計數體積不準。2.細胞計數儀,如Cellometer自動細胞計數儀。它是假定計數的顯微鏡視野相當于細胞計數板一個計數池的面積,沒有考慮液體深度,而且顯微鏡放大或縮小視野面積會改變,所以計數樣本體積更不準確。3.流式細胞計數儀,以B.Dtc20-automated-cell-counter 為例,是根據庫爾特原理,以顆粒大小相當于細胞大小為判定標準計數細胞,非細胞顆粒會當成細胞計數,細胞在生長分裂過程中體積會有變化,過大與過小的細胞會漏計數,不同類型細胞體積可以一樣大,所以細胞計數不準確。這三類細胞計數器還存在一個共同問題:計數的細胞樣品不可以回收使用。這個細胞計數杯計數方法解決了傳統細胞計數方法存在的問題。這個細胞計數杯還沒有商品,希望有興趣有能力的廠家生產出來,推廣應用。
1. 細胞計數杯的結構形態
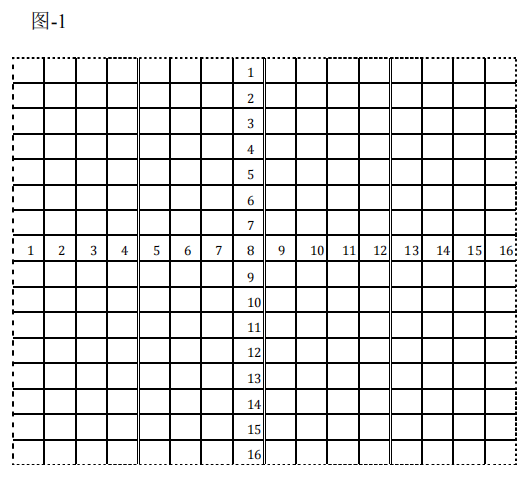
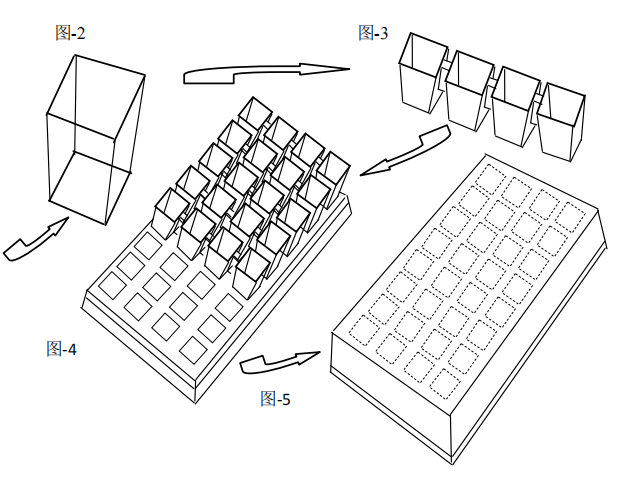
細胞計數杯是一個方形塑料杯,杯底內表面積(不含壁厚)4.0mm×4.0mm,杯口面積6.0mm×6.0mm,杯高10.0mm,體積160微升,圖-2。杯底表面用橫豎16×16條線分割成256個方格,標有縱橫序列號,雙線將方格分成16個計數區,虛線是邊線,可以劃線或不劃線,圖-1。4個計數杯一組連在一起,圖-3。連體計數杯排列在鑄有配套方孔的杯架上,隨意取放,圖-4。一個整體透明杯蓋蓋在連體計數杯與杯架上,圖-5。圖-5是實際應用形式,置于顯微鏡上計數細胞。整套杯具無菌處理,一次性使用。計數杯架4行8列,也可以做成4行4列。質量要點:(1)杯底和杯蓋一定要完全透明,(2)杯底要平整,四周不能隆起或凹下,(3)杯底劃線要均勻,方格不能有大有小。
2. 細胞計數杯的使用方法
2.1. 基本使用方法
取10→100微升(任意選定)計數樣品,輕輕放入計數杯中,將計數杯置于倒置顯微鏡平臺上,待細胞完全沉入杯底后,按方格順序計數細胞。每個方格里的細胞數不能密度太大,1~10較好。令記錄到的總細胞數為C,樣本體積為v,稀釋倍數為f
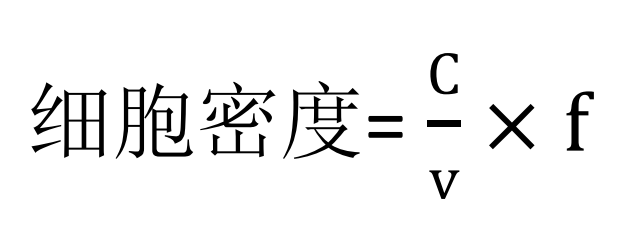
2.2. 快速統計學計數方法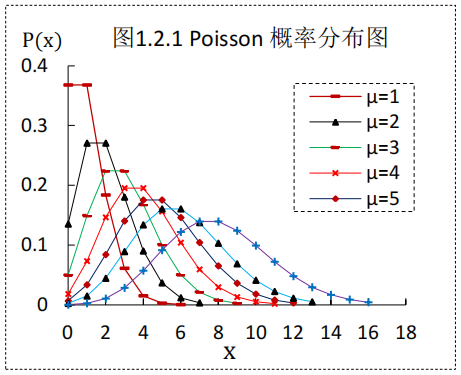
計數256個方格內的細胞,需要5~10分鐘時間,細胞密度大需要更長時間。在兩種情況下可以選擇用快速統計學方法計數。平均每個方格里的細胞數稱為細胞均數,用μ表示,(1)μ大于8個,(2)μ小于3個。例如(1)的情況,μ=10,把2560個細胞放入計數杯里,平均每個格子里10個細胞,但不會每個格子里都是10個細胞,有的多于10個,有的少于10個,大多數接近于10個,屬于正態分布。(2)的情況,μ=1,把256個細胞放入計數杯里,平均每個格子里1個細胞,但不會每個格子里都是1個細胞,有的0個,有的1個,或2個,或3個...,接近于0個和1個的較多,屬于偏態分布。圖1畫出了μ小于8的幾種情況。圖1表明,μ大于5趨近于正態分布,μ大于8屬于正態分布。
2.2.1正態分布情況計數方法
細胞計數時,如果每個方格里的細胞數多于10個,可以按正態分布計數細胞密度。隨機在16個計數區里選擇n(5095%)。
細胞密度=μ×256×1/v×f
2.2.2偏態分布情況計數方法
細胞計數時,如果每個方格里的細胞數少于3個,可以按偏態分布計數細胞密度。Poisson分布函數適合處理概率很低(P<<1)和樣品個數很多n>>30的低頻率偏態分布事件。Poisson分布函數如下式,

公式(1)里的符號用細胞計數術語表示,
x是每個方格內的細胞數,x= 0, 1, 2, 3 … 20
P(x)是一個方格內有x陽性細胞的概率。
e為自然對數的底e = 2.71828.
μ為平均一個方格內的細胞數, μ稱為單位均數。
細胞計數,一個方格為一計數單位,計數的方格數為單位數,用n表示。用rx表示一個方格內有x細胞的方格數,方格內有x細胞的概率為

方格內有0細胞的概率為

偏態分布rx決定于μ值。μ一定,r0,r1,r2 ..., 與 P(0), P(1), P(2) ..., 就一定。反過來rx和P(X)一定,μ也就一定。選擇用P(0)或P(1)或P(2)..., 來確定μ是一樣的。用公式(1)計算的是P(X)理論值,用公式(2)計算的P(X)是實驗值,兩者等價。用公式(1)計算P(X)時,由于涉及到指數和排列組合運算,相當麻煩。如果選擇x=0,P(X)=P(0),求解μ就非常簡單,
P(0)為陰性單位概率,將x = 0, 代入(1) 式

兩邊取自然對數,lnP(0) = -μ. (1) 式與(2)式等價,于是

(5)式表示:單位均數等于陰性單位概率的負對數。這表示只要有了P(0)由(5)式即可求出單位均數μ.有了n和r0,就有了P(0)和μ. 256×μ是總細胞數。
細胞密度=μ×256×1/v×f
這樣,計數細胞變成了計數空格,計數空格比計數細胞容易的多。例如μ=1,大約256個格中有256個細胞,由(5)式可以計算出空格r0=94。計數256個細胞至少需要5分鐘,計數94個空格有1分鐘就夠了。
2.3.細胞計數杯是驗證傳統細胞計數方法可信度的實用工具
細胞計數杯計數方法有兩大優勢,(1)計數細胞量大,一般在500以上,大到3000,(2)計數細胞樣本體積大,10~100微升是傳統計數板計數樣本體積0.1微升的100~1000倍。計數細胞數量越多,體積越大,計數越準確,所以細胞計數杯計數得到的細胞密度準確度很高,經過驗證達到98%以上,其他細胞計數方法都達不到。因此可以用作細胞計數準確性比較的參照標準,驗證傳統細胞計數方法的準確度。驗證方法就是用同一個細胞樣本,用不同方法計數,然后比較結果
2.4細胞計數杯是驗證統計學誤差理論的實用工具
統計學是一門應用非常廣泛的學科。誤差分析理論是其應用基礎,誤差公式是用數學理論推導出來的,老師講授,學生接受,很少有人用實驗做驗證,不是沒有人想驗證,主要是沒有簡單實用的驗證工具和方法。一般實驗方法,因為無法獲得標準的真實值而無法驗證。有了細胞計數杯,這個問題就解決了。統計學誤差分析理論有兩套系統:正態分布系統和偏態分布系統。
2.4.1正態分布誤差分析公式
(1)樣本抽樣誤差
標準差是表示一套變量離散程度的指標,均數和標準差結合起來說明變量的分布情況。總體標準差公式,

式中σ-總體標準差,x-變量值, μ-總體均數,N-變量個數。
由于很難獲得μ值,一般用樣本標準差估計總體標準差。
樣本標準差公式:

式中S-樣本標準差,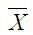 -樣本均數, n-變量個數。(7)式運算比較麻煩,一般轉換成下式計算,
-樣本均數, n-變量個數。(7)式運算比較麻煩,一般轉換成下式計算,

(2)均數抽樣誤差
從同一個總體中隨機抽取同樣大小的樣本,由于存在抽樣誤差,各樣本均數不會相同。以樣本均數做變量值計算樣本均數變異情況的標準差,稱為均數標準誤。統計學理論表明,均數標準誤( )與總體標準差(σx)及樣本大小(n)的關系如下,
)與總體標準差(σx)及樣本大小(n)的關系如下,

實際上總體標準差(σ)很難得到,只能獲得樣本誤差(S),一般用樣本誤差代替總體標準差(σ)求得均數標準誤的估計值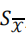 ,
,

2.4.2偏態分布誤差分析公式
處理偏態分布事件的公式主要有二項式分布和Poisson分布。以Poisson分布為例,Poisson分布如(1)式,其均數誤差公式為,

樣本均數標準誤估計值為

2.4.3均數的可信限
從均數為μ,方差為σ2的正態分布總體中隨機抽取n樣本,則樣本均數近似以總體均數為中心的正態分布。根據正態分布理論,樣本均數( )與總體均數(μ)有如下關系
)與總體均數(μ)有如下關系

2.5如何用細胞計數杯計數方法驗證正態分布誤差理論的正確性
2.5.1驗證統計學處理的隨機事件是否符合正態分布或偏態分布狀態
方法是將細胞計數杯放置水平,輕輕放入細胞,使之慢慢沉降,隨機分布在杯底。然后計數方格中的細胞,細胞數相同的歸為一組,稱為頻數,最后按頻數大小排序,畫在二維坐標圖上。根據頻數排序和頻數圖,確定均數大于10的符不符合正態分布理論,均數小于3的符不符合偏態分布理論。
2.5.2驗證統計學抽樣誤差理論的方法
舉一個例子,調查中國家庭收入平均水平。不可能對全部家庭都做調查,可以在全國各省區隨機分別抽取300戶家庭,合計有10000個家庭。一個辦法是收集每個家庭的收入,計算家庭收入平均值和離散狀況(樣本誤差)。另一個辦法是將10000個家庭隨機分成100個或200個樣本,計算樣本均數,然后求解均數標準誤。統計分析結果得到一個樣本均數( ,μ)和標準差(S,Sμ)和均數標準誤估計值(
,μ)和標準差(S,Sμ)和均數標準誤估計值( )。統計分析結果對不對?符不符合真實情況?可信度多大?本例因為拿不到總體均數μ值,沒有參照標準作,說不清楚。只能認為理論公式正確,結果就正確。公式正不正確?需要實踐證明,至今未見過實驗證明。細胞計數杯計數方法,因為能夠把計數杯里的細胞全部準確計數出來,可以拿到總體均數μ值,所以能夠驗證誤差公式的正確性。方法是,先按2.4.1方法將每個方格中的細胞計數出來,計算總體均數μ值,然后用誤差公式計算誤差值,誤差大小與樣本數(n)有關系,應該計算不同樣本數的誤差值。最后將結果帶入公式 (15),公式成立證明正確,否則不正確,進而確定什么情況下正確,什么情況下不正確。
)。統計分析結果對不對?符不符合真實情況?可信度多大?本例因為拿不到總體均數μ值,沒有參照標準作,說不清楚。只能認為理論公式正確,結果就正確。公式正不正確?需要實踐證明,至今未見過實驗證明。細胞計數杯計數方法,因為能夠把計數杯里的細胞全部準確計數出來,可以拿到總體均數μ值,所以能夠驗證誤差公式的正確性。方法是,先按2.4.1方法將每個方格中的細胞計數出來,計算總體均數μ值,然后用誤差公式計算誤差值,誤差大小與樣本數(n)有關系,應該計算不同樣本數的誤差值。最后將結果帶入公式 (15),公式成立證明正確,否則不正確,進而確定什么情況下正確,什么情況下不正確。
驗證統計學理論目的不只是證誤,而是提供一個實證和感性認識,讓學習者從理論和實踐兩方面認識統計學理論,加深對理論的理解,應用起來心里踏實。
3.細胞計數杯的應用前景
上述情況表明,細胞計數杯計數方法避免了傳統細胞計數方法存在的問題,大大提高了細胞計數的準確性,對于細胞學研究和臨床應用具有重要意義,其計數準確性和多用途優勢使其具有廣闊的應用前景,特別是對統計學理論的驗證功能,開設統計學課程的大、中、專院校都需要這樣的工具和方法。
1. 細胞計數杯的結構形態
細胞計數杯是一個方形塑料杯,杯底內表面積(不含壁厚)4.0mm×4.0mm,杯口面積6.0mm×6.0mm,杯高10.0mm,體積160微升,圖-2。杯底表面用橫豎16×16條線分割成256個方格,標有縱橫序列號,雙線將方格分成16個計數區,虛線是邊線,可以劃線或不劃線,圖-1。4個計數杯一組連在一起,圖-3。連體計數杯排列在鑄有配套方孔的杯架上,隨意取放,圖-4。一個整體透明杯蓋蓋在連體計數杯與杯架上,圖-5。圖-5是實際應用形式,置于顯微鏡上計數細胞。整套杯具無菌處理,一次性使用。計數杯架4行8列,也可以做成4行4列。質量要點:(1)杯底和杯蓋一定要完全透明,(2)杯底要平整,四周不能隆起或凹下,(3)杯底劃線要均勻,方格不能有大有小。


2. 細胞計數杯的使用方法
2.1. 基本使用方法
取10→100微升(任意選定)計數樣品,輕輕放入計數杯中,將計數杯置于倒置顯微鏡平臺上,待細胞完全沉入杯底后,按方格順序計數細胞。每個方格里的細胞數不能密度太大,1~10較好。令記錄到的總細胞數為C,樣本體積為v,稀釋倍數為f
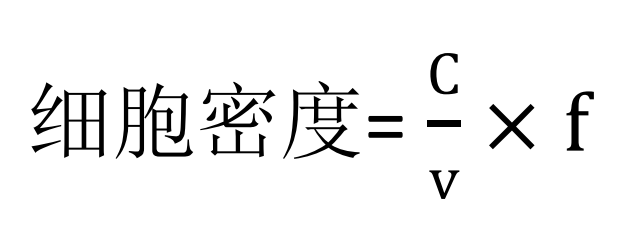
2.2. 快速統計學計數方法

計數256個方格內的細胞,需要5~10分鐘時間,細胞密度大需要更長時間。在兩種情況下可以選擇用快速統計學方法計數。平均每個方格里的細胞數稱為細胞均數,用μ表示,(1)μ大于8個,(2)μ小于3個。例如(1)的情況,μ=10,把2560個細胞放入計數杯里,平均每個格子里10個細胞,但不會每個格子里都是10個細胞,有的多于10個,有的少于10個,大多數接近于10個,屬于正態分布。(2)的情況,μ=1,把256個細胞放入計數杯里,平均每個格子里1個細胞,但不會每個格子里都是1個細胞,有的0個,有的1個,或2個,或3個...,接近于0個和1個的較多,屬于偏態分布。圖1畫出了μ小于8的幾種情況。圖1表明,μ大于5趨近于正態分布,μ大于8屬于正態分布。
2.2.1正態分布情況計數方法
細胞計數時,如果每個方格里的細胞數多于10個,可以按正態分布計數細胞密度。隨機在16個計數區里選擇n(5095%)。
細胞密度=μ×256×1/v×f
2.2.2偏態分布情況計數方法
細胞計數時,如果每個方格里的細胞數少于3個,可以按偏態分布計數細胞密度。Poisson分布函數適合處理概率很低(P<<1)和樣品個數很多n>>30的低頻率偏態分布事件。Poisson分布函數如下式,

公式(1)里的符號用細胞計數術語表示,
x是每個方格內的細胞數,x= 0, 1, 2, 3 … 20
P(x)是一個方格內有x陽性細胞的概率。
e為自然對數的底e = 2.71828.
μ為平均一個方格內的細胞數, μ稱為單位均數。
細胞計數,一個方格為一計數單位,計數的方格數為單位數,用n表示。用rx表示一個方格內有x細胞的方格數,方格內有x細胞的概率為

方格內有0細胞的概率為

偏態分布rx決定于μ值。μ一定,r0,r1,r2 ..., 與 P(0), P(1), P(2) ..., 就一定。反過來rx和P(X)一定,μ也就一定。選擇用P(0)或P(1)或P(2)..., 來確定μ是一樣的。用公式(1)計算的是P(X)理論值,用公式(2)計算的P(X)是實驗值,兩者等價。用公式(1)計算P(X)時,由于涉及到指數和排列組合運算,相當麻煩。如果選擇x=0,P(X)=P(0),求解μ就非常簡單,
P(0)為陰性單位概率,將x = 0, 代入(1) 式

兩邊取自然對數,lnP(0) = -μ. (1) 式與(2)式等價,于是

(5)式表示:單位均數等于陰性單位概率的負對數。這表示只要有了P(0)由(5)式即可求出單位均數μ.有了n和r0,就有了P(0)和μ. 256×μ是總細胞數。
細胞密度=μ×256×1/v×f
這樣,計數細胞變成了計數空格,計數空格比計數細胞容易的多。例如μ=1,大約256個格中有256個細胞,由(5)式可以計算出空格r0=94。計數256個細胞至少需要5分鐘,計數94個空格有1分鐘就夠了。
2.3.細胞計數杯是驗證傳統細胞計數方法可信度的實用工具
細胞計數杯計數方法有兩大優勢,(1)計數細胞量大,一般在500以上,大到3000,(2)計數細胞樣本體積大,10~100微升是傳統計數板計數樣本體積0.1微升的100~1000倍。計數細胞數量越多,體積越大,計數越準確,所以細胞計數杯計數得到的細胞密度準確度很高,經過驗證達到98%以上,其他細胞計數方法都達不到。因此可以用作細胞計數準確性比較的參照標準,驗證傳統細胞計數方法的準確度。驗證方法就是用同一個細胞樣本,用不同方法計數,然后比較結果
2.4細胞計數杯是驗證統計學誤差理論的實用工具
統計學是一門應用非常廣泛的學科。誤差分析理論是其應用基礎,誤差公式是用數學理論推導出來的,老師講授,學生接受,很少有人用實驗做驗證,不是沒有人想驗證,主要是沒有簡單實用的驗證工具和方法。一般實驗方法,因為無法獲得標準的真實值而無法驗證。有了細胞計數杯,這個問題就解決了。統計學誤差分析理論有兩套系統:正態分布系統和偏態分布系統。
2.4.1正態分布誤差分析公式
(1)樣本抽樣誤差
標準差是表示一套變量離散程度的指標,均數和標準差結合起來說明變量的分布情況。總體標準差公式,

式中σ-總體標準差,x-變量值, μ-總體均數,N-變量個數。
由于很難獲得μ值,一般用樣本標準差估計總體標準差。
樣本標準差公式:

式中S-樣本標準差,
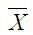 -樣本均數, n-變量個數。(7)式運算比較麻煩,一般轉換成下式計算,
-樣本均數, n-變量個數。(7)式運算比較麻煩,一般轉換成下式計算,
(2)均數抽樣誤差
從同一個總體中隨機抽取同樣大小的樣本,由于存在抽樣誤差,各樣本均數不會相同。以樣本均數做變量值計算樣本均數變異情況的標準差,稱為均數標準誤。統計學理論表明,均數標準誤(
 )與總體標準差(σx)及樣本大小(n)的關系如下,
)與總體標準差(σx)及樣本大小(n)的關系如下,
實際上總體標準差(σ)很難得到,只能獲得樣本誤差(S),一般用樣本誤差代替總體標準差(σ)求得均數標準誤的估計值
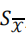 ,
,
2.4.2偏態分布誤差分析公式
處理偏態分布事件的公式主要有二項式分布和Poisson分布。以Poisson分布為例,Poisson分布如(1)式,其均數誤差公式為,

樣本均數標準誤估計值為

2.4.3均數的可信限
從均數為μ,方差為σ2的正態分布總體中隨機抽取n樣本,則樣本均數近似以總體均數為中心的正態分布。根據正態分布理論,樣本均數(
 )與總體均數(μ)有如下關系
)與總體均數(μ)有如下關系
2.5如何用細胞計數杯計數方法驗證正態分布誤差理論的正確性
2.5.1驗證統計學處理的隨機事件是否符合正態分布或偏態分布狀態
方法是將細胞計數杯放置水平,輕輕放入細胞,使之慢慢沉降,隨機分布在杯底。然后計數方格中的細胞,細胞數相同的歸為一組,稱為頻數,最后按頻數大小排序,畫在二維坐標圖上。根據頻數排序和頻數圖,確定均數大于10的符不符合正態分布理論,均數小于3的符不符合偏態分布理論。
2.5.2驗證統計學抽樣誤差理論的方法
舉一個例子,調查中國家庭收入平均水平。不可能對全部家庭都做調查,可以在全國各省區隨機分別抽取300戶家庭,合計有10000個家庭。一個辦法是收集每個家庭的收入,計算家庭收入平均值和離散狀況(樣本誤差)。另一個辦法是將10000個家庭隨機分成100個或200個樣本,計算樣本均數,然后求解均數標準誤。統計分析結果得到一個樣本均數(
 ,μ)和標準差(S,Sμ)和均數標準誤估計值(
,μ)和標準差(S,Sμ)和均數標準誤估計值( )。統計分析結果對不對?符不符合真實情況?可信度多大?本例因為拿不到總體均數μ值,沒有參照標準作,說不清楚。只能認為理論公式正確,結果就正確。公式正不正確?需要實踐證明,至今未見過實驗證明。細胞計數杯計數方法,因為能夠把計數杯里的細胞全部準確計數出來,可以拿到總體均數μ值,所以能夠驗證誤差公式的正確性。方法是,先按2.4.1方法將每個方格中的細胞計數出來,計算總體均數μ值,然后用誤差公式計算誤差值,誤差大小與樣本數(n)有關系,應該計算不同樣本數的誤差值。最后將結果帶入公式 (15),公式成立證明正確,否則不正確,進而確定什么情況下正確,什么情況下不正確。
)。統計分析結果對不對?符不符合真實情況?可信度多大?本例因為拿不到總體均數μ值,沒有參照標準作,說不清楚。只能認為理論公式正確,結果就正確。公式正不正確?需要實踐證明,至今未見過實驗證明。細胞計數杯計數方法,因為能夠把計數杯里的細胞全部準確計數出來,可以拿到總體均數μ值,所以能夠驗證誤差公式的正確性。方法是,先按2.4.1方法將每個方格中的細胞計數出來,計算總體均數μ值,然后用誤差公式計算誤差值,誤差大小與樣本數(n)有關系,應該計算不同樣本數的誤差值。最后將結果帶入公式 (15),公式成立證明正確,否則不正確,進而確定什么情況下正確,什么情況下不正確。驗證統計學理論目的不只是證誤,而是提供一個實證和感性認識,讓學習者從理論和實踐兩方面認識統計學理論,加深對理論的理解,應用起來心里踏實。
3.細胞計數杯的應用前景
上述情況表明,細胞計數杯計數方法避免了傳統細胞計數方法存在的問題,大大提高了細胞計數的準確性,對于細胞學研究和臨床應用具有重要意義,其計數準確性和多用途優勢使其具有廣闊的應用前景,特別是對統計學理論的驗證功能,開設統計學課程的大、中、專院校都需要這樣的工具和方法。
相關文章閱讀鏈接:現行細胞計數方法存在的問題與解決辦法
歡迎掃描下方微信二維碼參與討論


Copyright(C) 1998-2025 生物器材網 電話:021-64166852;13621656896 E-mail:info@bio-equip.com